Graph Networks

Item-Item Co-Occurrence Graph

The item-item co-occurrence graph can be defined as an undirected graph $\mathcal{G = \{V, E\}}$, where $\mathcal{V}$ is the node set and $\mathcal{E}$ is the edge set. Each node in $𝑣 \in \mathcal{V}$ denotes an item. For user $𝑢 \in \mathcal{U}$, if two items $𝑣_0$ and $𝑣_1$ co-occur in his historical behavior sequence $\mathcal{B_𝑢}$, then the triplet $(𝑣_0, 𝑣_1, 𝑤) \in \mathcal{E}$. $𝑤$ denotes the co-occurrence times.

In practice, to construct an item-item co-occurrence graph, we set a sliding window and slide it on behavior sequences of all users. Each pair of items within the window are connected by an undirected edge. The weight of each edge is assigned as the total number of occurrences of the two connected items in all users’ behaviors.

Triangles

Triangle is an important structure in complex graph analysis in different fields, such as social networks and protein networks. Many existing works in graph theory have mentioned the properties of triangles. For instance, the homophily of triangles indicates the nodes in a triangle are often relatively similar. Triangles are also used to address some of the biases in existing CTR models.

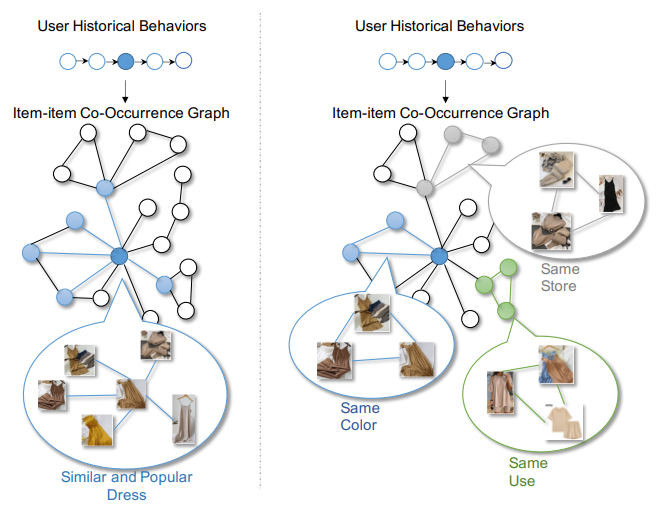
Standard CTR methods are biased towards the similar and popular items in the left figure. Triangle-based methods introduces different triangles as diverse interest units, such as skirts of the same color, store and use in the right figure. source.

In an item-item co-occurrence graph $\mathcal{G = \{V, E\}}$, for node $𝑣 \in \mathcal{V}$, we denote the set of its $K$-order ($K$>0) neighbor nodes as $\mathcal{V}_𝑣$. For three nodes $𝑣_0, 𝑣_1,\ \text{and}\ 𝑣_2 \in \mathcal{V}_𝑣$, we define the triplet $𝑡_𝑟 = (𝑣_0, 𝑣_1, 𝑣_2)$ as a triangle only if $(𝑣_0, 𝑣_1), (𝑣_0, 𝑣_2), and (𝑣_1, 𝑣_2) \in \mathcal{E}$.

The number of triangles can increase exponentially with the number of nodes. Thus, to effectively incorporate triangle structure information, we set $𝐾$ as a relative small number. Moreover, for a target node, since the influence of triangles of different distances is also distinct, we further introduce the definition of k-order triangles. k-Order Triangle: For node $𝑣 \in \mathcal{V}$, given a triangle $(𝑣_0, 𝑣_1, 𝑣_2)$, if the shortest distance from these three nodes to 𝑣 is 𝑘, then we define this triplet as a k-order triangle of 𝑣. Generally speaking, the triangle order 𝑘 is a natural number, which is smaller than the order of the neighborhood $𝐾$.